Revision as of 10:50, 2 December 2013

Go to root: PhD-3D-Object-Tracking

Rendering of a point cloud, showing a desktop.

All right: in the previous tutorial you installed OpenNI and PCL. You managed to get your device working. You compiled and ran the example program, watched as it fetched one frame after another, and even saved a couple of point clouds to disk. Now you may be wondering "What about now? What use depth sensors are? What can I do with point clouds?"

Well, depth cameras have a lot of useful applications. For example, you could use them as motion tracking hardware and save you thousands of dollars in professional gear. The original Kinect was actually designed as an alternative to physical controllers (i.e., gamepads) in games. Hand gestures can also be recognized, so people have managed to successfully implement control interfaces similar to what could be seen in Minority Report.

Working low-level with point clouds offers interesting possibilities too. As they are essentially a 3D "scan" or the scene, you could capture your whole room as a continuous 3D mesh, then import it in your modelling software of choice and use it as a reference for a better reconstruction. You could use it to measure distances, or detect obstacles, for a robot navigation system. But the most exciting alternative by far, and the one where most of the research is being focused on, is to perform 3D object recognition and pose estimation, even in real time. This allows a robot to fulfill tasks like going to the kitchen to get you a cup of coffee.

Most of the advanced stuff that can be done with a point cloud requires some previous steps, like filtering, reconstruction or normal estimation. In this tutorial, I will introduce you to the basics of point cloud processing, and leave the complicated methods for the next tutorial. I will explain what every technique does and what it should be used for, and include PCL code snippets so you can check how to implement it in your programs.

Point clouds

First, a little explanation. A point cloud as taken from a depth sensor consists of a series of points in 3D space, as simple as that. A "pcl::PointCloud<PointT>" object stores the points inside a "std::vector<PointT>" structure. The cloud object exposes some functions that let you get information about them, like the point count. As you can see, the class is templated so you can instantiate it for many types of points. For example, "PointXYZ", which stores three floats for the X, Y and Z coordinates, and "PointXYZRGB", which also stores color (texture) information for each point, the kind we would get with Kinect or Xtion RGB-D cameras. A list of point types and a basic description of the cloud object are available on PCL's website.

Once you have the cloud in memory, you can perform many operations with it. You can, of course, save them to disk, read them back, or concatenate several of them together. In order to select a subset of points, you can make use of indices, which contain a list of points from the original cloud. Many algorithms work with indices, or produce them as output. With the "ExtractIndices" class you create a second cloud that contains only the referenced points, or invert the selection and copy those not indexed.

When clouds are saved to disk, a PCD (Point Cloud Data) file is produced. You can choose to do it so in binary or plain text format. The first one is faster to work with, whereas the second one will let you to inspect the cloud by opening it with a common text editor. If you do so, you may see something like this:

# .PCD v.7 − Point Cloud Data file format
VERSION .7
FIELDS x y z
SIZE 4 4 4
TYPE F F F
WIDTH 2
HEIGHT 1
VIEWPOINT 0 0 0 1 0 0 0
POINTS 2
DATA ascii
0.73412 -1.12643 0.82218
0.44739 -0.34735 -0.04624

This tells us that the cloud consist of 2 points of type "PointXYZ" (because each point has only 3 fields; the X, Y and Z coordinates, each stored in a 4-byte float), and lists their coordinates. It also stores the viewport information (the relative position of the points to the sensor) as a translation quaternion. Knowing the position of the camera can be useful for certain procedures like normal estimation.

Feature estimation

A feature of a point is some characteristic that can help us to tell it apart from a different point. Of course, you could say that the XYZ coordinates would be characteristic enough, but when interpolating the data of two different, yet corresponding, clouds, they become useless. We need something better, that will have similar values when computed for the same spot of a surface in both sets.

Normals are an example of a very simple feature. 3D features will be important later in our tutorials, when we talk about descriptors (more detailed "signatures" of points used for close matching).

Normal estimation

As you may remember from geometry class, the normal of a plane is an unit vector that is perpendicular to it. The normal of a surface at a point is defined as the vector that is perpendicular to the plane that is tangent to the surface at the point. Surface normals can be calculated for the points of a cloud, too. It is considered a feature, albeit not a very discriminative one.

I will not go into detail with the math of the estimation method, but you just have to know that is uses the nearest neighbors (the points that are closest to the one we are calculating the normal for) to find out the tangent plane and the normal vector. You can customize the method with the search radius (think about a sphere of that radius, centered in the point; all neighboring points that lie within will be used for the computation) and the viewpoint (by default, the output normals will be directionless; by supposing that all vectors must point towards the camera - because otherwise they would belong to surfaces that are not visible from the sensor - they can all be re-oriented accordingly).

Normals are also important because they give us information about the curvature of the surface at some point, which can be used to our advantage. Many of PCL's algorithms will require us to provide the normals of the input cloud. To estimate them, you can use the following code:

#include <pcl/io/pcd_io.h>
#include <pcl/features/normal_3d.h>
#include <boost/thread/thread.hpp>
#include <pcl/visualization/pcl_visualizer.h>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	// Object for storing the normals.
	pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
	
	// Read a PCD file from disk.
	try
	{
		pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud);
	}
	catch (pcl::PCLException e)
	{
		return -1;
	}
	
	// Object for normal estimation.
	pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
	normalEstimation.setInputCloud(cloud);
	// For every point, use all neighbors in a radius of 3cm.
	normalEstimation.setRadiusSearch(0.03);
	// A kd-tree is a data structure that makes searches efficient. More about it later.
	// The normal estimation object will use it to find nearest neighbors.
	pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>());
	normalEstimation.setSearchMethod(kdtree);
	
	// Calculate the normals.
	normalEstimation.compute(*normals);
	
	// Visualize them.
	boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer("Normals"));
	viewer->addPointCloud<pcl::PointXYZ>(cloud, "cloud");
	// Display one normal out of 20, as a line of length 3cm.
	viewer->addPointCloudNormals<pcl::PointXYZ, pcl::Normal>(cloud, normals, 20, 0.03, "normals");
	while (!viewer->wasStopped())
  	{
		viewer->spinOnce(100);
		boost::this_thread::sleep(boost::posix_time::microseconds(100000));
	}
	
	return 0;
}

As you can see, normals are stored in "PointCloud" objects too, instantiated to the "Normal" type. If you ever extract some indices from a cloud before feeding them to an algorithm, be sure to do the same with the normals. I have not bothered to include proper error/argument checking, nor have I made use of the "setViewPoint()" function, but you get the idea. Be sure to check the PCL API every time I introduce you to one of its classes or methods.

Visualization of the normals computed for a point cloud.

Decomposition

When I talk about decomposition, I mean the process of creating an ordered, organized data structure from the points of the cloud, with some purpose in mind like making further analysis easier, or performing filters.

k-d tree

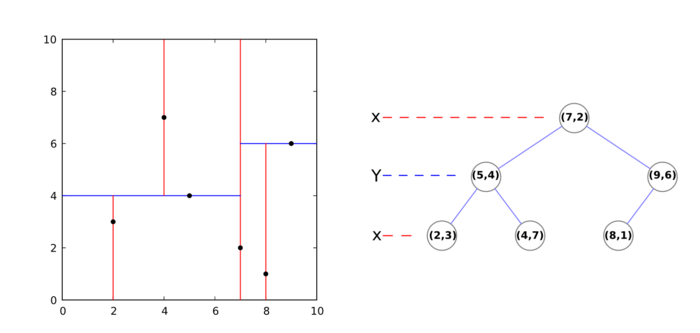
A k-d tree (k-dimensional tree) is a data structure that organizes a set of points in a k-dimensional space, in a way that makes range search operations very efficient (for example, finding the nearest neighbor of a point, which is the point that is closest to it in space; or finding all neighbors within a radius).

It is a binary tree, that is, every non-leaf node in it has two children nodes, the "left" and "right" ones. Each level splits space on a specific dimension. For example, in 3-dimensional space, at the root node (first level) all children would be split based on the first dimension, X (points having coordinates with greater X values would go to the right subtree, points with lesser values to the left one). At the second level (the nodes we just created), the split would be done on the Y axis, following the same criteria. At the third level (the grandchildren), we would use the Z axis. At the fourth level, we would get back to the X axis, and so on. Usually, the median point is chosen to be root at every level.

Example of a 2D kd-tree (image from Wikimedia Commons).

In PCL, creating a k-d tree from a cloud is a straightforward and fast operation:

#include <pcl/io/pcd_io.h>
#include <pcl/search/kdtree.h>

#include <iostream>
#include <vector>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	
	// Read a PCD file from disk.
	try
	{
		pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud);
	}
	catch (pcl::PCLException e)
	{
		return -1;
	}
	  
	// kd-tree object.
	pcl::search::KdTree<pcl::PointXYZ> kdtree;
	kdtree.setInputCloud(cloud);
	
	// We will find the 5 nearest neighbors of this point
	// (it does not have to be one of the cloud's, we can use any coordinate).
	pcl::PointXYZ point;
	point.x = 0.0524343;
	point.y = -0.58016;
	point.z = 1.776;
	// This vector will store the output neighbors.
	std::vector<int> pointIndices(5);
	// This vector will store their squared distances to the search point.
	std::vector<float> squaredDistances(5);
	// Perform the search, and print out results.
	if (kdtree.nearestKSearch(point, 5, pointIndices, squaredDistances) > 0)
	{
		std::cout << "5 nearest neighbors of the point:" << std::endl;
		for (size_t i = 0; i < pointIndices.size(); ++i)
			std::cout << "\t" << cloud->points[pointIndices[i]].x
			          << " " << cloud->points[pointIndices[i]].y
			          << " " << cloud->points[pointIndices[i]].z
			          << " (squared distance: " << squaredDistances[i] << ")" << std::endl;
	}
	
	// Now we find all neighbors within 3cm of the point
	// (inside a sphere of radius 3cm centered at the point).
	if (kdtree.radiusSearch(point, 0.03, pointIndices, squaredDistances) > 0)
	{
		std::cout << "Neighbors within 3cm:" << std::endl;
		for (size_t i = 0; i < pointIndices.size(); ++i)
			std::cout << "\t" << cloud->points[pointIndices[i]].x
			          << " " << cloud->points[pointIndices[i]].y
			          << " " << cloud->points[pointIndices[i]].z
			          << " (squared distance: " << squaredDistances[i] << ")" << std::endl;
	}
	
	return 0;
}

Another alternative would be "KdTreeFLANN", which makes use of FLANN (Fast Library for Approximate Nearest Neighbors).

Octree

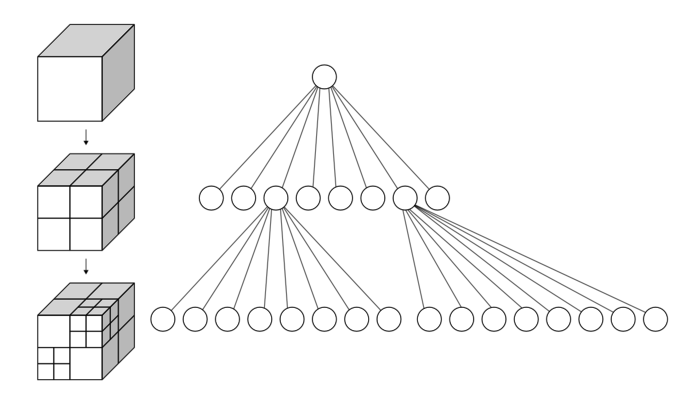
Like the k-d tree, the octree is an hierarchical tree data structure useful for searches, but also compression or downsampling. Each octree node (called a voxel, a term that will sound familiar for users of 3D engines, and which could be described as a "3D pixel", that is, a cube) has either eight children or no children. The root node describes a cubic bounding box which encapsulates all points. At every level, it becomes subdivided by a factor of 2 which results in an increased voxel resolution. That way, we can selectively give more resolution to certain zones.

Depiction of an octree (image from Wikimedia Commons).

Downsampling will be covered in a different section, so now I will show you how to perform searches with an octree:

#include <pcl/io/pcd_io.h>
#include <pcl/octree/octree.h>

#include <iostream>
#include <vector>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	
	// Read a PCD file from disk.
	try
	{
		pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud);
	}
	catch (pcl::PCLException e)
	{
		return -1;
	}
	  
	// Octree object, with a maximum resolution of 128
	// (resolution at lowest octree level).
	pcl::octree::OctreePointCloudSearch<pcl::PointXYZ> octree(128);
	octree.setInputCloud(cloud);
	octree.addPointsFromInputCloud();
	
	// We will find all neighbors within the same voxel as this point.
	// (it does not have to be one of the cloud's, we can use any coordinate).
	pcl::PointXYZ point;
	point.x = 0.0524343;
	point.y = -0.58016;
	point.z = 1.776;
	// This vector will store the output neighbors.
	std::vector<int> pointIndices;
	// Perform the search, and print out results.
	if (! octree.voxelSearch(point, pointIndices) > 0)
	{
		std::cout << "Neighbors in the same voxel:" << std::endl;
		for (size_t i = 0; i < pointIndices.size(); ++i)
			std::cout << "\t" << cloud->points[pointIndices[i]].x
			          << " " << cloud->points[pointIndices[i]].y
			          << " " << cloud->points[pointIndices[i]].z << std::endl;
	}
	
	// We will find the 5 nearest neighbors of the point.
	// This vector will store their squared distances to the search point.
	std::vector<float> squaredDistances;
	if (octree.nearestKSearch(point, 5, pointIndices, squaredDistances) > 0)
	{
		std::cout << "5 nearest neighbors of the point:" << std::endl;
		for (size_t i = 0; i < pointIndices.size(); ++i)
			std::cout << "\t" << cloud->points[pointIndices[i]].x
			          << " " << cloud->points[pointIndices[i]].y
			          << " " << cloud->points[pointIndices[i]].z
			          << " (squared distance: " << squaredDistances[i] << ")" << std::endl;
	}
	
	// Now we find all neighbors within 3cm of the point
	// (inside a sphere of radius 3cm centered at the point).
	// The point DOES have to belong in the cloud.
	if (octree.radiusSearch(point, 0.03, pointIndices, squaredDistances) > 0)
	{
		std::cout << "Neighbors within 3cm:" << std::endl;
		for (size_t i = 0; i < pointIndices.size(); ++i)
			std::cout << "\t" << cloud->points[pointIndices[i]].x
			          << " " << cloud->points[pointIndices[i]].y
			          << " " << cloud->points[pointIndices[i]].z
			          << " (squared distance: " << squaredDistances[i] << ")" << std::endl;
	}
	
	return 0;
}

As you can see, the code is mostly interchangeable with the one of the kd-tree.

On the other hand, this is the code needed to compress and decompress a point cloud with PCL:

#include <pcl/io/pcd_io.h>
#include <pcl/compression/octree_pointcloud_compression.h>
#include <boost/thread/thread.hpp>
#include <pcl/visualization/pcl_visualizer.h>

int
main(int argc, char** argv)
{
	// Object for storing the point clouds.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointCloud<pcl::PointXYZ>::Ptr decompressedCloud(new pcl::PointCloud<pcl::PointXYZ>);
	
	// Read a PCD file from disk.
	try
	{
		pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud);
	}
	catch (pcl::PCLException e)
	{
		return -1;
	}
	
	// Octree compressor object.
	// Check /usr/include/pcl-<version>/pcl/compression/compression_profiles.h for more profiles.
	// The second parameter enables the output of information.
	pcl::io::OctreePointCloudCompression<pcl::PointXYZ> octreeCompression(pcl::io::MED_RES_ONLINE_COMPRESSION_WITHOUT_COLOR, true);
	// Stringstream that will hold the compressed cloud.
	std::stringstream compressedData;
	
	// Compress the cloud (you would save the stream to disk).
	octreeCompression.encodePointCloud(cloud, compressedData);
	
	// Decompress the cloud.
	octreeCompression.decodePointCloud(compressedData, decompressedCloud);
	
	// Display the decompressed cloud.
	boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer("Octree compression"));
	viewer->addPointCloud<pcl::PointXYZ>(decompressedCloud, "cloud");
	while (!viewer->wasStopped())
  	{
		viewer->spinOnce(100);
		boost::this_thread::sleep(boost::posix_time::microseconds(100000));
	}
	
	return 0;
}

As you can see, the process has decreased the amount of points in the cloud. The default parameters of the "OctreePointCloudCompression" object establish an octree resolution (at lowest level) of 1cm, and a coordinate precision of 1mm. These values can of course be changed to suit your needs, but simplying the cloud in this way is an useful operation that we will cover later.

Filtering

The raw point cloud, as returned from the sensor, usually needs some kind of polishing before being handed to processing algorithms. Normally, this is due to the low precision of the sensor, which leads to noise, incorrect measurements, holes in surfaces... Sometimes it is just the opposite: the cloud has so many points that processing it would take forever. Luckily, several filtering methods exist to "fix" many recurring errors in point clouds.

Passthrough filter

A passthrough filter will remove any point from the cloud whose values do not fall in a certain range, user-given. For example, if you wanted to discard all points farther away than, say, 3 meters, you would run the filter on the Z coordinate with a range of [0,3]. This filter can be useful to discard unneeded objects from the cloud, but you may have to adapt a different reference frame if the default one (relative to the sensor) is not fitting. For example, filtering on the Y value to remove all points not sitting on a table will yield unwanted results of the camera was at an odd angle.

#include <pcl/io/pcd_io.h>
#include <pcl/filters/passthrough.h>

int
main(int argc, char** argv)
{
	// Object for storing the point clouds.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointCloud<pcl::PointXYZ>::Ptr filteredCloud(new pcl::PointCloud<pcl::PointXYZ>);
	
	// Read a PCD file from disk.
	try
	{
		pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud);
	}
	catch (pcl::PCLException e)
	{
		return -1;
	}
	
	// Filter object.
	pcl::PassThrough<pcl::PointXYZ> filter;
	filter.setInputCloud(cloud);
	// Filter out all points with Z values not in the [0-2] range.
	filter.setFilterFieldName("z");
	filter.setFilterLimits(0.0, 2.0);

	filter.filter(*filteredCloud);
	
	return 0;
}

The "setFilterLimitsNegative()" function (not seen in the example) will tell the filter object whether to return the points inside the range ("false", the default value) or outside it ("true").

Conditional removal

Another way of getting the exact same result than with the previous example would be to use a conditional removal filter. We can build any kind of condition we want for the values of the point:

#include <pcl/io/pcd_io.h>
#include <pcl/filters/conditional_removal.h>

int
main(int argc, char** argv)
{
	// Object for storing the point clouds.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointCloud<pcl::PointXYZ>::Ptr filteredCloud(new pcl::PointCloud<pcl::PointXYZ>);
	
	// Read a PCD file from disk.
	try
	{
		pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud);
	}
	catch (pcl::PCLException e)
	{
		return -1;
	}
	
	// We must build a condition.
	// And "And" condition requires all tests to check true. "Or" conditions also available.
	pcl::ConditionAnd<pcl::PointXYZ>::Ptr condition(new pcl::ConditionAnd<pcl::PointXYZ>());
	// First test, the point's Z value must be greater than (GT) 0.
	condition->addComparison(pcl::FieldComparison<pcl::PointXYZ>::ConstPtr(new pcl::FieldComparison<pcl::PointXYZ>("z", pcl::ComparisonOps::GT, 0.0)));
	// Second test, the point's Z value must be less than (LT) 2.
	condition->addComparison(pcl::FieldComparison<pcl::PointXYZ>::ConstPtr(new pcl::FieldComparison<pcl::PointXYZ>("z", pcl::ComparisonOps::LT, 2.0)));
	// Checks available: GT, GE, LT, LE, EQ.
	
	// Filter object.
	pcl::ConditionalRemoval<pcl::PointXYZ> filter(condition);
	filter.setInputCloud(cloud);
	// If true, points that do not pass the filter will be set to a certain value (default NaN).
	// If false, they will be just removed, but that could break the structure of the cloud
	// (organized clouds are clouds taken from camera-like sensors that return a matrix-like image).
	filter.setKeepOrganized(true);
	// If keep organized was set true, points that failed the test will have their Z value set to this.
	filter.setUserFilterValue(0.0);
	
	filter.filter(*filteredCloud);
	
	return 0;
}

Outlier removal

Outliers are lonely points that are spread here and there in the cloud, like annoying mosquitoes. They are the product of the sensor's inaccuracy, which registers measurements where there should not be any. Outliers are considered undesired noise because they can introduce errors in calculations, like for example the normal estimation. Hence, trimming they out of the cloud will not only make computations faster (because the less points there are, the less time it takes, as we will see with downsampling) but also help us get more precise values.

Radius-based

The radius-based outlier removal is the simplest method of all. You must specify a search radius and the minimum number of neighbors than a point must have to avoid being labelled as outlier. The algorithm will then iterate through all points (which can be slow in if the cloud is big) and perform the check: if less than that number of points are found within the radius, it is removed.

#include <pcl/io/pcd_io.h>
#include <pcl/filters/radius_outlier_removal.h>

int
main(int argc, char** argv)
{
	// Object for storing the point clouds.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointCloud<pcl::PointXYZ>::Ptr filteredCloud(new pcl::PointCloud<pcl::PointXYZ>);
	
	// Read a PCD file from disk.
	try
	{
		pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud);
	}
	catch (pcl::PCLException e)
	{
		return -1;
	}
	
	// Filter object.
	pcl::RadiusOutlierRemoval<pcl::PointXYZ> filter;
	filter.setInputCloud(cloud);
	// Every point must have 10 neighbors within 15cm, or it will be removed.
	filter.setRadiusSearch(0.15);
	filter.setMinNeighborsInRadius(10);
	
	filter.filter(*filteredCloud);
	
	return 0;
}

All PCL classes that inherit from "pcl::FilterIndices" (like "pcl::RadiusOutlierRemoval") provide the function "setNegative()", which if set to true, makes the filter return the points that did NOT pass the filter.

Statistical

The statistical outlier removal process is a bit more refined. First, for every point, the mean distance to its K neighbors is computed. Then, if we asume that the result is a normal (gaussian) distribution with a mean μ and a standard deviation σ, we can deem it safe to remove all points with mean distances that fall out of the global mean plus deviation. Basically, it runs a statistical analysis of the distances between neighboring points, and trims all which are not considered "normal" (you define what "normal" is with the parameters of the algorithm).

#include <pcl/io/pcd_io.h>
#include <pcl/filters/statistical_outlier_removal.h>
 
int
main(int argc, char** argv)
{
	// Object for storing the point clouds.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointCloud<pcl::PointXYZ>::Ptr filteredCloud(new pcl::PointCloud<pcl::PointXYZ>);
	
	// Read a PCD file from disk.
	try
	{
		pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud);
	}
	catch (pcl::PCLException e)
	{
		return -1;
	}
	
	// Filter object.
	pcl::StatisticalOutlierRemoval<pcl::PointXYZ> filter;
	filter.setInputCloud(cloud);
	// Set number of neighbors to consider to 50.
	filter.setMeanK(50);
	// Set standard deviation multiplier to 1.
	// Points with a distance larger than 1 standard deviation of the mean distance will be outliers.
	filter.setStddevMulThresh(1.0);
	
	filter.filter(*filteredCloud);
	
	return 0;
}

You can make use of "setNegative()" with this filter too.

Go to root: PhD-3D-Object-Tracking

Links to articles:

PCL/OpenNI tutorial 1: First steps

PCL/OpenNI tutorial 2: Cloud processing (basic)

PCL/OpenNI tutorial 3: Cloud processing (advanced)

PCL/OpenNI tutorial 4: 3D object recognition (descriptors)

PCL/OpenNI tutorial 5: 3D object recognition (detection and pose estimation)

PCL/OpenNI troubleshooting