Go to root: PhD-3D-Object-Tracking

Most of the techniques seen in the previous tutorial focused on preprocessing, that is, performing certain operations on the cloud to get it ready for further analysis or work. Downsampling, removing outliers, smoothing the surfaces, estimating the normals...

This new tutorial will teach you many interesting things that can be done with point clouds after the preparation step, such as registration, segmentation and model matching.

Registration

Registration is the technique of aligning two point clouds, like pieces of a puzzle. To be precise, the algorithm finds a set of correspondences between them, which would mean that there is an area of the scene that has been captured in both clouds. A linear transformation is then computed, which outputs a matrix that contains a rotation and a translation. These are the operations that you would apply to one of the clouds so it would get in place with respect to the other, with the intersecting areas overlapping.

The best results are achieved with clouds that are very similar, so you should try to minimize the transformations between them. Meaning, do not run like crazy with a Kinect in your hands, grabbing frames, and expect PCL to match the clouds. It is better to move the sensor gingerly and at steady intervals. If you use a robotic arm or a rotating tabletop with precise angles, even better.

Registration is a very useful technique because it lets you retrieve full, complete and continous models of a scene or object. It is also expensive for the CPU. Optimizations have been developed that allow to do cloud matching in real time with the GPU, like KinFu does.

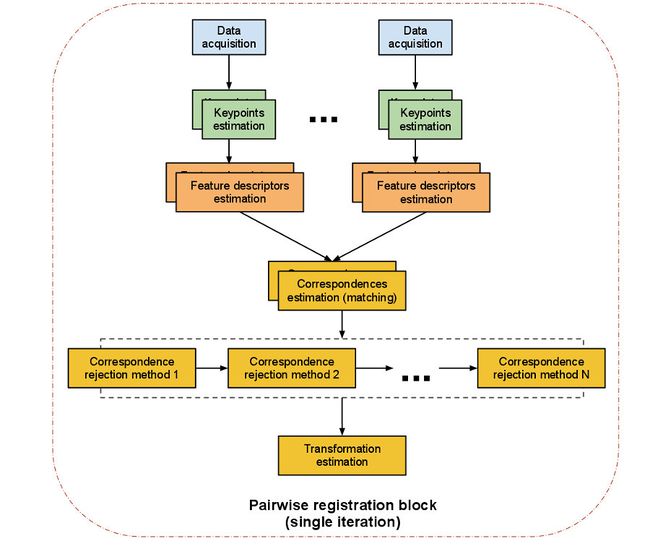
Flowchart diagram showing an iteration of the registration algorithm (image from http://pointclouds.org/).

The previous diagram illustrates how the procedure is done. There are mainly two different methods to choose from:

ICP registration: ICP stands for Iterative Closest Point. It is an algorithm that will find the best transformation that minimizes the distance from the source point cloud to the target one. The problem is that it will do it by associating every point of the source cloud to its "twin" in the target cloud in a linear way, so it can be considered a brute force method. It the clouds are too big, the algorithm will take its time to finish, so try downsampling them first.
Feature-based registration: the algorithm finds a set of keypoints in each cloud, computes a descriptor for each (we mentioned what descriptors were in the previous tutorial; they are like individual signatures of points), and then performs a search to see if the clouds have keypoints in common. If true, a transformation is computed. For accurate results, enough correspondences must be found. This method is (or should be) faster than the first, because matching is only done for the keypoints, not the whole cloud.

The second method is basically identical to the 3D object recognition problem, so we will not look into it here. Features, descriptors and recognition will be dealt with in the next tutorials.

Tutorial: The PCL Registration API

Iterative Closest Point (ICP)

PCL offers several implementations of the ICP algorithm. We will see the general, unoptimized one, but you may want to try one of the optimized variants listed below in the API section. The code for aligning (registering) two point clouds is the following:

#include <pcl/io/pcd_io.h>
#include <pcl/registration/icp.h>

#include <iostream>

int
main(int argc, char** argv)
{
	// Objects for storing the point clouds.
	pcl::PointCloud<pcl::PointXYZ>::Ptr sourceCloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointCloud<pcl::PointXYZ>::Ptr targetCloud(new pcl::PointCloud<pcl::PointXYZ>);
	pcl::PointCloud<pcl::PointXYZ>::Ptr finalCloud(new pcl::PointCloud<pcl::PointXYZ>);

	// Read two PCD files from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *sourceCloud) != 0)
	{Source point cloud.
		return -1;
	}
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[2], *targetCloud) != 0)
	{
		return -1;
	}

	// ICP object.
	pcl::IterativeClosestPoint<pcl::PointXYZ, pcl::PointXYZ> registration;
	registration.setInputSource(sourceCloud);
	registration.setInputTarget(targetCloud);
	
	registration.align(*finalCloud);
	if (registration.hasConverged())
	{
		std::cout << "ICP converged." << std::endl
		          << "The score is " << registration.getFitnessScore() << std::endl;
		std::cout << "Transformation matrix:" << std::endl;
		std::cout << registration.getFinalTransformation() << std::endl;
	}
	else std::cout << "ICP did not converge." << std::endl;

	return 0;
}

The cloud saved in "finalCloud" is the same as "sourceCloud" (it has the same points), but the transformation found by ICP has been applied, so when visualized next to "targetCloud" they should match properly (errors are inevitable and depend of many factors, like the quality of the sensor, the distance between the clouds, the algorithm used...).

Source point cloud.
Target point cloud.
Both clouds shown together before registration.
Both clouds shown together after registration.

Input: Source cloud, Target cloud
Output: Registered source cloud, Transformation matrix
Tutorial: How to use iterative closest point, How to incrementally register pairs of clouds. How to use Normal Distributions Transform
API: pcl::IterativeClosestPoint, pcl::IterativeClosestPointWithNormals, pcl::IterativeClosestPointNonLinear, pcl::NormalDistributionsTransform
Download

Segmentation

Segmentation consists of breaking the cloud apart in different pieces or sections: groups of points called clusters (which is why it is also referred to as clustering). The idea is to divide it in several parts to be processed independently. Ideally, every cluster would belong to the logical notion of "object". For example, for a cloud that shows 3 boxes on a table, 4 clusters would be created: one for the table, and one for each of the boxes.

There are many segmentation techniques, each one with its own criteria for grouping points together. Some consider the distance between points, some take into account the normals, or even the texture, too. Here I will give you an overview of each one.

Segmentation, together with all other methods seen so far, will allow you to retrieve the models of individual objects from a scene. Also, it is possible to segment certain shapes like planes or cylinders, but this will be seen in another section.

Euclidean

Euclidean segmentation is the simplest of all. It checks the distance between two points. If it is less than a threshold, both are considered to belong in the same cluster. It works like a flood fill algorithm: a point in the cloud is "marked" as "chosen" for the cluster. Then, it spreads like a virus to all other points that are near enough, and from those to even more points, until none new can be added. Then, a new cluster is initialized, and the procedure starts again with the remaining unmarked points.

In PCL, Euclidean segmentation is done as follows:

#include <pcl/io/pcd_io.h>
#include <pcl/segmentation/extract_clusters.h>

#include <iostream>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// kd-tree object for searches.
	pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
	kdtree->setInputCloud(cloud);

	// Euclidean clustering object.
	pcl::EuclideanClusterExtraction<pcl::PointXYZ> clustering;
	// Set cluster tolerance to 2cm (small values may cause objects to be divided
	// in several clusters, whereas big values may join objects in a same cluster).
	clustering.setClusterTolerance(0.02);
	// Set the minimum and maximum number of points that a cluster can have.
	clustering.setMinClusterSize(100);
	clustering.setMaxClusterSize(25000);
	clustering.setSearchMethod(kdtree);
	clustering.setInputCloud(cloud);
	std::vector<pcl::PointIndices> clusters;
	clustering.extract(clusters);

	// For every cluster...
	int currentClusterNum = 1;
	for (std::vector<pcl::PointIndices>::const_iterator i = clusters.begin(); i != clusters.end(); ++i)
	{
		// ..add all its points to a new cloud...
		pcl::PointCloud<pcl::PointXYZ>::Ptr cluster(new pcl::PointCloud<pcl::PointXYZ>);
		for (std::vector<int>::const_iterator point = i->indices.begin(); point != i->indices.end(); point++)
			cluster->points.push_back(cloud->points[*point]);
		cluster->width = cluster->points.size();
		cluster->height = 1;
		cluster->is_dense = true;

		// ...and save it to disk.
		if (cluster->points.size() <= 0)
			break;
		std::cout << "Cluster " << currentClusterNum << " has " << cluster->points.size() << " points." << std::endl;
		std::string fileName = "cluster" + boost::to_string(currentClusterNum) + ".pcd";
		pcl::io::savePCDFileASCII(fileName, *cluster);

		currentClusterNum++;
	}

	return 0;
}

You may have to play with the cluster tolerance parameter until you get good results. Also, it is recommended to perform planar segmentation (we will see it later) to remove the floor and/or table(s) from the scene, or the results may be wrong.

After the program finishes, you can visualize all clusters at the same time with:

pcl_viewer cluster*

Original cloud.
Clusters recovered after Euclidean segmentation (each cluster is renderer with a different color).

Input: Points, Cluster tolerance, Minimum cluster size, Maximum cluster size
Output: Vector of Point indices (clusters)
Tutorial: Euclidean Cluster Extraction
API: pcl::EuclideanClusterExtraction
Download

Conditional

Conditional Euclidean segmentation works the same way as the standard one seen above, with one exception. Apart from the distance check, points need also to meet a special, custom requirement for them to be added to a cluster. This condition is user-specified. It boils down to this: for every pair of points (the first one, the seed, is being processed in this moment, the second one, candidate, is a neighbor of the former that is being tested) a custom function will be called. This function has a certain signature: it receives

a copy of the two points so we can perform our own tests, and
the squared distance

and returns a boolean value. If the value is true, the candidate may be added to the cluster. If false, it will not, even if it passed the distance check.

#include <pcl/io/pcd_io.h>
#include <pcl/segmentation/conditional_euclidean_clustering.h>

#include <iostream>

// If this function returns true, the candidate point will be added
// to the cluster of the seed point.
bool
customCondition(const pcl::PointXYZ& seedPoint, const pcl::PointXYZ& candidatePoint, float squaredDistance)
{
	// Do whatever you want here.
	if (candidatePoint.y < seedPoint.y)
		return false;
	
	return true;
}

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// Conditional Euclidean clustering object.
	pcl::ConditionalEuclideanClustering<pcl::PointXYZ> clustering;
	clustering.setClusterTolerance(0.02);
	clustering.setMinClusterSize(100);
	clustering.setMaxClusterSize(25000);
	clustering.setInputCloud(cloud);
	// Set the function that will be called for every pair of points to check.
	clustering.setConditionFunction(&customCondition);
	std::vector<pcl::PointIndices> clusters;
	clustering.segment(clusters);

	// For every cluster...
	int currentClusterNum = 1;
	for (std::vector<pcl::PointIndices>::const_iterator i = clusters.begin(); i != clusters.end(); ++i)
	{
		// ..add all its points to a new cloud...
		pcl::PointCloud<pcl::PointXYZ>::Ptr cluster(new pcl::PointCloud<pcl::PointXYZ>);
		for (std::vector<int>::const_iterator point = i->indices.begin(); point != i->indices.end(); point++)
			cluster->points.push_back(cloud->points[*point]);
		cluster->width = cluster->points.size();
		cluster->height = 1;
		cluster->is_dense = true;

		// ...and save it to disk.
		if (cluster->points.size() <= 0)
			break;
		std::cout << "Cluster " << currentClusterNum << " has " << cluster->points.size() << " points." << std::endl;
		std::string fileName = "cluster" + boost::to_string(currentClusterNum) + ".pcd";
		pcl::io::savePCDFileASCII(fileName, *cluster);

		currentClusterNum++;
	}

	return 0;
}

The condition that is implemented above (checking if the candidate's Y coordinate is lower than the seed's) does not make a lot of sense, but I just wanted you to understand how the method works.

If you pass "true" to the constructor of "pcl::ConditionalEuclideanClustering", the object will store the clusters that were discarded for being too small or too big. You can later retrieve them with the getRemovedClusters() function.

Input: Points, Cluster tolerance, Minimum cluster size, Maximum cluster size, Custom check function
Output: Vector of Point indices (clusters)
Tutorial: Conditional Euclidean Clustering
API: pcl::ConditionalEuclideanClustering
Download

Region growing

This type of segmentation (which is also a greedy-like, flood fill approach like the Euclidean one) groups together points that check a smoothness constraint. The angle between their normals and the difference of curvatures are checked to see if they could belong to the same smooth surface. Think about a box laying on a table: with Euclidean segmentation, both would be considered to be in the same cluster because they are "touching". With region growing segmentation, this would not happen, because there is a 90° (with ideal normal estimation, that is) difference between the normals of a point in the table and another one in the box's lateral.

#include <pcl/io/pcd_io.h>
#include <pcl/search/kdtree.h>
#include <pcl/features/normal_3d.h>
#include <pcl/segmentation/region_growing.h>

#include <iostream>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	// Object for storing the normals.
	pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// kd-tree object for searches.
	pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
	kdtree->setInputCloud(cloud);
	
	// Estimate the normals.
	pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
	normalEstimation.setInputCloud(cloud);
	normalEstimation.setRadiusSearch(0.03);
	normalEstimation.setSearchMethod(kdtree);
	normalEstimation.compute(*normals);

	// Region growing clustering object.
	pcl::RegionGrowing<pcl::PointXYZ, pcl::Normal> clustering;
	clustering.setMinClusterSize(100);
	clustering.setMaxClusterSize(10000);
	clustering.setSearchMethod(kdtree);
	clustering.setNumberOfNeighbours(30);
	clustering.setInputCloud(cloud);
	clustering.setInputNormals(normals);
	// Set the angle in radians that will be the smoothness threshold
	// (the maximum allowable deviation of the normals).
	clustering.setSmoothnessThreshold(7.0 / 180.0 * M_PI); // 7 degrees.
	// Set the curvature threshold. The disparity between curvatures will be
	// tested after the normal deviation check has passed.
	clustering.setCurvatureThreshold(1.0);

	std::vector <pcl::PointIndices> clusters;
	clustering.extract(clusters);

	// For every cluster...
	int currentClusterNum = 1;
	for (std::vector<pcl::PointIndices>::const_iterator i = clusters.begin(); i != clusters.end(); ++i)
	{
		// ..add all its points to a new cloud...
		pcl::PointCloud<pcl::PointXYZ>::Ptr cluster(new pcl::PointCloud<pcl::PointXYZ>);
		for (std::vector<int>::const_iterator point = i->indices.begin(); point != i->indices.end(); point++)
			cluster->points.push_back(cloud->points[*point]);
		cluster->width = cluster->points.size();
		cluster->height = 1;
		cluster->is_dense = true;

		// ...and save it to disk.
		if (cluster->points.size() <= 0)
			break;
		std::cout << "Cluster " << currentClusterNum << " has " << cluster->points.size() << " points." << std::endl;
		std::string fileName = "cluster" + boost::to_string(currentClusterNum) + ".pcd";
		pcl::io::savePCDFileASCII(fileName, *cluster);

		currentClusterNum++;
	}

	return 0;
}

Input: Points, Minimum cluster size, Maximum cluster size, Neighbor count, Search method, Normals, Smoothness threshold, Curvature threshold
Output: Vector of Point indices (clusters)
Tutorial: Region growing segmentation
API: pcl::RegionGrowing
Download