PCL/OpenNI tutorial 4: 3D object recognition (descriptors)

From robotica.unileon.es
Revision as of 11:00, 21 March 2014 by Victorm (talk | contribs)

Jump to: navigation, search

Go to root: PhD-3D-Object-Tracking


It is time to learn the basics of one of the most interesting applications of point cloud processing: 3D object recognition. Akin to 2D recognition, this technique relies on finding good keypoints (characteristic points) in the cloud, and matching them to a set of previously saved ones. But 3D has several advantages over 2D: namely, we will be able to estimate with decent accuracy the exact position and orientation of the object, relative to the sensor. Also, 3D object recognition tends to be more robust to clutter (crowded scenes where objects in the front occluding objects in the background). And finally, having information about the object's shape will help with collision avoidance or grasping operations.

In this first tutorial we will see what descriptors are, how many types are there available in PCL, and how to compute them.

Overview

The basis of 3D object recognition is to find a set of correspondences between two different clouds, one of them containing the object we are looking for. In order to do this, we need a way to compare points in an unambiguous manner. Until now, we have worked with points that store the XYZ coordinates, the RGB color... but none of those properties are unique enough. In two sequential scans, two points could share the same coordinates despite belonging to different surfaces, and using the color information takes us back to 2D recognition, will all the lightning related problems.

In a previous tutorial, we talked about features, before introducing the normals. Normals are an example of feature, because they encode information about the vicinity of the point. That is, the neighboring points are taken into account when computing it, giving us an idea of how the surrounding surface is. But this is not enough. For a feature to be optimal, it must meet the following criteria:

  1. It must be robust to transformations: rigid transformations (the ones that do not change the distance between points) like translations and rotations must not affect the feature. Even if we play with the cloud a bit beforehand, there should be no difference.
  2. It must be robust to noise: measurement errors that cause noise should not change the feature estimation much.
  3. It must be resolution invariant: if sampled with different density (like after performing downsampling), the result must be identical or similar.

This is where descriptors come in. They are more complex (and precise) signatures of a point, that encode a lot of information about the surrounding geometry. The purpose is to unequivocally identify a point across multiple point clouds, no matter the noise, resolution or transformations. Also, some of them capture additional data about the object they belong to, like the viewpoint (that lets us retrieve the pose).

Finding correspondences between point features of two clouds (image from http://pointclouds.org/).

There are many 3D descriptors implemented into PCL. Each one has its own method for computing unique values for a point. Some use the difference between the angles of the normals of the point and its neighbors, for example. Others use the distances between the points. Because of this, some are inherently better or worse for certain purposes. A given descriptor may be scale invariant, and another one may be better with occlusions and partial views of objects. Which one you choose depends on what you want to do.

After calculating the necessary values, an additional step is performed to reduce the descriptor size: the result is binned into an histogram. To do this, the value range of each variable that makes up the descriptor is divided into n subdivisions, and the number of occurrences in each one is counted. Try to imagine a descriptor that computes a single variable, that ranges from 1 to 100. We choose to create 10 bins for it, so the first bin would gather all occurrences between 1 and 10, the second from 11 to 20, and so on. We look at the value of the variable for the first point-neighbor pair, and it is 27, so we increment the value of the third bin by 1. We keep doing this until we get a final histogram for that keypoint. The bin size must be carefully chosen depending on how descriptive that variable is (the variables do not have to share the same number of bins).

Descriptors can be classified in two main categories: global and local. The process for computing and using each one (recognition pipeline) is different, so each will be explained in its own section in this article.


Local descriptors

Local descriptors are computed for individual points that we give as input. They have no notion of what an object is, they just describe how the local geometry is around that point. Usually, it is your task to choose which points you want a descriptor to be computed for: the keypoints. Most of the time, you can get away by just performing a downsampling and choosing all remaining points.

Local descriptors are used for object recognition and registration. Now we will see which ones are implemented into PCL.

PFH

PFH stands for Point Feature Histogram. It is one of the most important descriptors offered by PCL and the basis of others such as FPFH. The PFH tries to capture information of the geometry surrounding the point by analyzing the difference between the directions of the normals in the vicinity (and because of this, an imprecise normal estimation may produce low-quality descriptors).

First, the algorithm pairs all points in the vicinity (not just the chosen keypoint with its neighbors, but also the neighbors with themselves). Then, for each pair, a fixed coordinate frame is computed from their normals. With this frame, the difference between the normals can be encoded with 3 angular variables. These variables, together with the euclidean distance between the points, are saved, and then binned to an histogram when all pairs have been computed. The final descriptor is the concatenation of the histograms of each variable (4 in total).

Computing descriptors in PCL is very easy, and the PFH is not an exception: 

#include <pcl/io/pcd_io.h>
#include <pcl/features/normal_3d.h>
#include <pcl/features/pfh.h>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	// Object for storing the normals.
	pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
	// Object for storing the PFH descriptors for each point.
	pcl::PointCloud<pcl::PFHSignature125>::Ptr descriptors(new pcl::PointCloud<pcl::PFHSignature125>());

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}
	
	// Note: you would usually perform downsampling now. It has been omitted here
	// for simplicity, but be aware that computation can take a long time.

	// Estimate the normals.
	pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
	normalEstimation.setInputCloud(cloud);
	normalEstimation.setRadiusSearch(0.03);
	pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
	normalEstimation.setSearchMethod(kdtree);
	normalEstimation.compute(*normals);

	// PFH estimation object.
	pcl::PFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::PFHSignature125> pfh;
	pfh.setInputCloud(cloud);
	pfh.setInputNormals(normals);
	pfh.setSearchMethod(kdtree);
	// Search radius, to look for neighbors. Note: the value given here has to be
	// larger than the radius used to estimate the normals.
	pfh.setRadiusSearch(0.05);

	pfh.compute(*descriptors);

	return 0;
}

As you can see, PCL uses the "PFHSignature125" type to save the descriptor to. This means that the descriptor's size is 125 (the dimensionality of the feature vector). Dividing a feature in D dimensional space in B divisions requires a total of BD bins. The original proposal makes use of the distance between the points, but the implementation of PCL does not, as it was not considered discriminative enough (specially in 2.5D scans, where the distance between points increases the further away from the sensor). Hence, the remaining features (with one dimension each) can be divided in 5 divisions, resulting in a 125-dimensional (53) vector.

The final object that stores the computed descriptors can be handled like a normal cloud (even saved to, or read from, disk), and it has the same number of "points" than the original one. The "PFHSignature125" object at position 0, for example, stores the PFH descriptor for the "PointXYZ" point at the same position in the cloud.

For additional details about the descriptor, check the original publications listed below, or PCL's tutorial.


FPFH

PFH gives accurate results, but it has a drawback: it is too computationally expensive to perform at real time. For a cloud of n keypoints with k neighbors considered, it has a complexity of O(nk2). Because of this, a derived descriptor was created, named FPFH (Fast Point Feature Histogram).

The FPFH considers only the direct connections between the current keypoint and its neighbors, removing additional links between neighbors. This takes the complexity down to O(nk). Because of this, the resulting histogram is referred to as SPFH (Simplified Point Feature Histogram). The reference frame and the angular variables are computed as always.

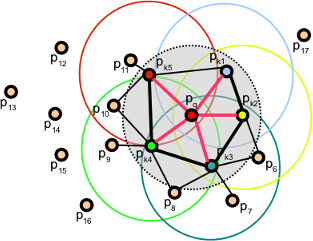
Point pairs established when computing the FPFH for a point (image from http://pointclouds.org).

To account for the loss of these extra connections, an additional step takes place after all histograms have been computed: the SPFHs of a point's neighbors are "merged" with its own, weighted according to the distance. This has the effect of giving a point surface information of points as far away as 2 times the radius used. Finally, the 3 histograms (distance is not used) are concatenated to compose the final descriptor. 

#include <pcl/io/pcd_io.h>
#include <pcl/features/normal_3d.h>
#include <pcl/features/fpfh.h>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	// Object for storing the normals.
	pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
	// Object for storing the FPFH descriptors for each point.
	pcl::PointCloud<pcl::FPFHSignature33>::Ptr descriptors(new pcl::PointCloud<pcl::FPFHSignature33>());

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}
	
	// Note: you would usually perform downsampling now. It has been omitted here
	// for simplicity, but be aware that computation can take a long time.

	// Estimate the normals.
	pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
	normalEstimation.setInputCloud(cloud);
	normalEstimation.setRadiusSearch(0.03);
	pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
	normalEstimation.setSearchMethod(kdtree);
	normalEstimation.compute(*normals);

	// FPFH estimation object.
	pcl::FPFHEstimation<pcl::PointXYZ, pcl::Normal, pcl::FPFHSignature33> fpfh;
	fpfh.setInputCloud(cloud);
	fpfh.setInputNormals(normals);
	fpfh.setSearchMethod(kdtree);
	// Search radius, to look for neighbors. Note: the value given here has to be
	// larger than the radius used to estimate the normals.
	fpfh.setRadiusSearch(0.05);

	fpfh.compute(*descriptors);

	return 0;
}

An additional implementation of the FPFH estimation that takes advantage of multithreaded optimizations (with the OpenMP API) is available in the class "FPFHEstimationOMP". Its interface is identical to the standard unoptimized implementation. Using it will result in a big performance boost on multi-core systems, meaning faster computation times. Remember to include the header "fpfh_omp.h" instead.


RSD

The Radius-Based Surface Descriptor encodes the radial relationship of the point and its neighborhood. For every pair of the keypoint with a neighbor, the algorithm computes the distance between them, and the difference between their normals. Then, by assuming that both points lie on the surface of a sphere, said sphere is found by fitting not only the points, but also the normals (otherwise, there would be infinite possible spheres). Finally, from all the point-neighbor spheres, only the ones with the maximum and minimum radii are kept and saved to the descriptor of that point.

As you may have deduced already, when two points lie on a flat surface, the sphere radius will be infinite. If, on the other hand, they lie on the curved face of a cylinder, the radius will be more or less the same as that of the cylinder. This allows us to tell apart objects with RSD. The algorithm takes a parameter that sets the maximum radius at which the points will be considered to be part of a plane.

Currently, the RSD estimator class is not available in PCL because it lacked proper testing and documentation (for more details, see the issue or this post on the mailing list). When it is restored, I will provide a code snippet as always (I could do it now, but you would not be able to compile it).


3DSC

The 3D Shape Context is a descriptor that extends its existing 2D counterpart to the third dimension. It works by creating a support structure (a sphere, to be precise) centered at the point we are computing the descriptor for, with the given search radius. The "north pole" of that sphere (the notion of "up") is pointed to match the normal at that point. Then, the sphere is divided in 3D regions or bins. In the first 2 coordinates (azimuth and elevation) the divisions are equally spaced, but in the third (the radial dimension), divisions are logarithmically spaced so they are smaller towards the center. A minimum radius can be specified to prevent very small bins, that would be too sensitive to small changes in the surface.

Support structure to compute the 3DSC for a point (image from original paper).

For each bin, a weighted count is accumulated for every neighboring point that lies within. The weight depends on the volume of the bin and the local point density (number of points around the current neighbor). This gives the descriptor some degree of resolution invariance.

We have mentioned that the sphere is given the direction of the normal. This still leaves one degree of freedom (only two axes have been locked, the azimuth remains free). Because of this, the descriptor so far does not cope with rotation. To overcome this (so the same point in two different clouds has the same value), the support sphere is rotated around the normal N times (a number of degrees that corresponds with the divisions in the azimuth) and the process is repeated for each, giving a total of N descriptors for that point.

You can compute the 3DSC descriptor the following way: 

#include <pcl/io/pcd_io.h>
#include <pcl/features/normal_3d.h>
#include <pcl/features/3dsc.h>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	// Object for storing the normals.
	pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
	// Object for storing the 3DSC descriptors for each point.
	pcl::PointCloud<pcl::ShapeContext1980>::Ptr descriptors(new pcl::PointCloud<pcl::ShapeContext1980>());

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// Note: you would usually perform downsampling now. It has been omitted here
	// for simplicity, but be aware that computation can take a long time.

	// Estimate the normals.
	pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
	normalEstimation.setInputCloud(cloud);
	normalEstimation.setRadiusSearch(0.03);
	pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
	normalEstimation.setSearchMethod(kdtree);
	normalEstimation.compute(*normals);

	// 3DSC estimation object.
	pcl::ShapeContext3DEstimation<pcl::PointXYZ, pcl::Normal, pcl::ShapeContext1980> sc3d;
	sc3d.setInputCloud(cloud);
	sc3d.setInputNormals(normals);
	sc3d.setSearchMethod(kdtree);
	// Search radius, to look for neighbors. It will also be the radius of the support sphere.
	sc3d.setRadiusSearch(0.05);
	// The minimal radius value for the search sphere, to avoid being too sensitive
	// in bins close to the center of the sphere.
	sc3d.setMinimalRadius(0.05 / 10.0);
	// Radius used to compute the local point density for the neighbors
	// (the density is the number of points within that radius).
	sc3d.setPointDensityRadius(0.05 / 5.0);

	sc3d.compute(*descriptors);

	return 0;
}


USC

The Unique Shape Descriptor extends the 3DSC by defining a local reference frame, in order to provide an unique orientation for each point. This not only improves the accuracy of the descriptor, it also reduces its size, as computing multiple descriptors to account for orientation is no longer necessary.

You can check the second publication listed below to learn more about how the LRF is computed. 

#include <pcl/io/pcd_io.h>
#include <pcl/features/usc.h>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	// Object for storing the USC descriptors for each point.
	pcl::PointCloud<pcl::ShapeContext1980>::Ptr descriptors(new pcl::PointCloud<pcl::ShapeContext1980>());

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// Note: you would usually perform downsampling now. It has been omitted here
	// for simplicity, but be aware that computation can take a long time.

	// USC estimation object.
	pcl::UniqueShapeContext<pcl::PointXYZ, pcl::ShapeContext1980, pcl::ReferenceFrame> usc;
	usc.setInputCloud(cloud);
	// Search radius, to look for neighbors. It will also be the radius of the support sphere.
	usc.setRadiusSearch(0.05);
	// The minimal radius value for the search sphere, to avoid being too sensitive
	// in bins close to the center of the sphere.
	usc.setMinimalRadius(0.05 / 10.0);
	// Radius used to compute the local point density for the neighbors
	// (the density is the number of points within that radius).
	usc.setPointDensityRadius(0.05 / 5.0);
	// Set the radius to compute the Local Reference Frame.
	usc.setLocalRadius(0.05);

	usc.compute(*descriptors);

	return 0;
}


SHOT

SHOT stands for Signature of Histograms of Orientations. Like 3DSC, it encodes information about the topology (surface) withing a spherical support structure. This sphere is divided in 32 bins or volumes, with 8 divisions along the azimuth, 2 along the elevation, and 2 along the radius. For every volume, a one-dimensional local histogram is computed. The variable chosen is the angle between the normal of the keypoint and the current point within that volume (to be precise, the cosine, which was found to be better suitable).

Support structure to compute SHOT. Only 4 azimuth divisions are shown for clarity (image from original paper).

When all local histograms have been computed, they are stitched together in a final descriptor. Like the USC descriptor, SHOT makes use of a local reference frame, making it rotation invariant. It is also robust to noise and clutter. 

#include <pcl/io/pcd_io.h>
#include <pcl/features/normal_3d.h>
#include <pcl/features/shot.h>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	// Object for storing the normals.
	pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
	// Object for storing the SHOT descriptors for each point.
	pcl::PointCloud<pcl::SHOT352>::Ptr descriptors(new pcl::PointCloud<pcl::SHOT352>());

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// Note: you would usually perform downsampling now. It has been omitted here
	// for simplicity, but be aware that computation can take a long time.
	
	// Estimate the normals.
	pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
	normalEstimation.setInputCloud(cloud);
	normalEstimation.setRadiusSearch(0.03);
	pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
	normalEstimation.setSearchMethod(kdtree);
	normalEstimation.compute(*normals);

	// SHOT estimation object.
	pcl::SHOTEstimation<pcl::PointXYZ, pcl::Normal, pcl::SHOT352> shot;
	shot.setInputCloud(cloud);
	shot.setInputNormals(normals);
	// The radius that defines which of the keypoint's neighbors are described.
	// If too large, there may be clutter, and if too small, not enough points may be found.
	shot.setRadiusSearch(0.02);

	shot.compute(*descriptors);

	return 0;
}

Like with FPFH, a multithreading-optimized variant is available with "SHOTEstimationOMP", that makes use of OpenMP. You need to include the header "shot_omp.h". Also, another variant that uses the texture for matching is available, "SHOTColorEstimation", with an optimized version too (see the second publication for more details). It outputs a "SHOT1344" descriptor.


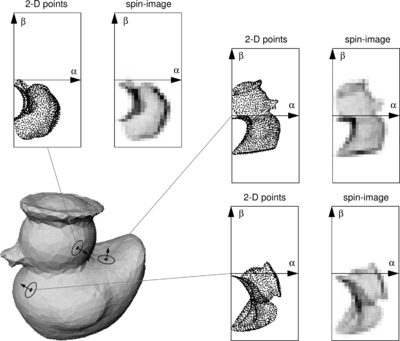
Spin image

The Spin Image (SI) is the oldest descriptor we are going to see here. It has been around since 1997, but it still sees some use for certain applications. It was originally designed to describe surfaces made by vertices, edges and polygons, but it has been since adapted for point clouds. The descriptor is unlike all others in that the output resembles an image that can be compared with another with the usual means.

The support structure used is a cylinder, centered at the point, with a given radius and height, and aligned with the normal. This cylinder is divided radially and vertically into volumes. For each one, the number of neighbors lying inside is added up, eventually producing a descriptor. Weighting and interpolation are used to improve the result. The final descriptor can be seen as a grayscale image where dark areas correspond to volumes with higher point density.

Spin images computed for 3 points of a model (image from original thesis).
#include <pcl/io/pcd_io.h>
#include <pcl/features/normal_3d.h>
#include <pcl/features/spin_image.h>

// A handy typedef.
typedef pcl::Histogram<153> SpinImage;

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);
	// Object for storing the normals.
	pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
	// Object for storing the spin image for each point.
	pcl::PointCloud<SpinImage>::Ptr descriptors(new pcl::PointCloud<SpinImage>());

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// Note: you would usually perform downsampling now. It has been omitted here
	// for simplicity, but be aware that computation can take a long time.
	
	// Estimate the normals.
	pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> normalEstimation;
	normalEstimation.setInputCloud(cloud);
	normalEstimation.setRadiusSearch(0.03);
	pcl::search::KdTree<pcl::PointXYZ>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZ>);
	normalEstimation.setSearchMethod(kdtree);
	normalEstimation.compute(*normals);

	// Spin image estimation object.
	pcl::SpinImageEstimation<pcl::PointXYZ, pcl::Normal, SpinImage> si;
	si.setInputCloud(cloud);
	si.setInputNormals(normals);
	// Radius of the support cylinder.
	si.setRadiusSearch(0.02);
	// Set the resolution of the spin image (the number of bins along one dimension).
	// Note: you must change the output histogram size to reflect this.
	si.setImageWidth(8);

	si.compute(*descriptors);

	return 0;
}

The Spin Image estimation object provides more methods for tuning the estimation, so checking the API is recommended.


RIFT

The Rotation-Invariant Feature Transform, like the spin image, takes some concepts from 2D features, in this case from the Scale-Invariant Feature Transform (SIFT). It is the only descriptor seen here that requires intensity information in order to compute it (it can be obtained from the RGB color values). This means, of course, that you will not be able to use RIFT with standard XYZ clouds, you also need the texture.

In the first step, a circular patch (with the given radius) is fitted on the surface the point lies on. This patch is divided into concentric rings, according to the chosen distance bin size. Then, an histogram is populated with all the point's neighbors lying inside a sphere centered at that point and with the mentioned radius. The distance and the orientation of the intensity gradient at each point are considered. To make it rotation invariant, the angle between the gradient orientation and the vector pointing outward from the center of the patch is measured.

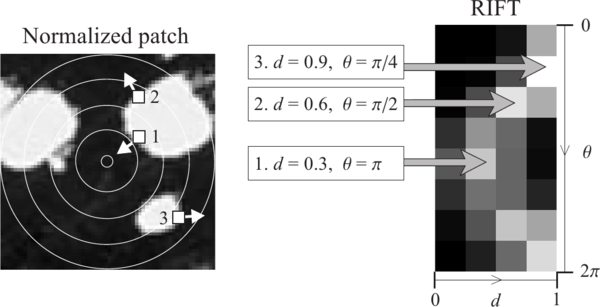
RIFT feature values at 3 different locations in the descriptor (image from original paper).

The authors' original implementation uses 4 rings and 8 histogram orientations, which produce a descriptor of size 32. RIFT is not robust to texture flipping, though this was never considered a big issue. 

#include <pcl/io/pcd_io.h>
#include <pcl/point_types_conversion.h>
#include <pcl/features/normal_3d.h>
#include <pcl/features/intensity_gradient.h>
#include <pcl/features/rift.h>

// A handy typedef.
typedef pcl::Histogram<32> RIFT32;

int
main(int argc, char** argv)
{
	// Object for storing the point cloud with color information.
	pcl::PointCloud<pcl::PointXYZRGB>::Ptr cloudColor(new pcl::PointCloud<pcl::PointXYZRGB>);
	// Object for storing the point cloud with intensity value.
	pcl::PointCloud<pcl::PointXYZI>::Ptr cloudIntensity(new pcl::PointCloud<pcl::PointXYZI>);
	// Object for storing the intensity gradients.
	pcl::PointCloud<pcl::IntensityGradient>::Ptr gradients(new pcl::PointCloud<pcl::IntensityGradient>);
	// Object for storing the normals.
	pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
	// Object for storing the RIFT descriptor for each point.
	pcl::PointCloud<RIFT32>::Ptr descriptors(new pcl::PointCloud<RIFT32>());

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZRGB>(argv[1], *cloudColor) != 0)
	{
		return -1;
	}

	// Note: you would usually perform downsampling now. It has been omitted here
	// for simplicity, but be aware that computation can take a long time.

	// Convert the RGB to intensity.
	pcl::PointCloudXYZRGBtoXYZI(*cloudColor, *cloudIntensity);

	// Estimate the normals.
	pcl::NormalEstimation<pcl::PointXYZI, pcl::Normal> normalEstimation;
	normalEstimation.setInputCloud(cloudIntensity);
	normalEstimation.setRadiusSearch(0.03);
	pcl::search::KdTree<pcl::PointXYZI>::Ptr kdtree(new pcl::search::KdTree<pcl::PointXYZI>);
	normalEstimation.setSearchMethod(kdtree);
	normalEstimation.compute(*normals);
	
	// Compute the intensity gradients.
	pcl::IntensityGradientEstimation<pcl::PointXYZI, pcl::Normal, pcl::IntensityGradient,
	                                 pcl::common::IntensityFieldAccessor<pcl::PointXYZI> > ge;
	ge.setInputCloud(cloudIntensity);
	ge.setInputNormals(normals);
	ge.setRadiusSearch(0.03);
	ge.compute(*gradients);

	// RIFT estimation object.
	pcl::RIFTEstimation<pcl::PointXYZI, pcl::IntensityGradient, RIFT32> rift;
	rift.setInputCloud(cloudIntensity);
	rift.setSearchMethod(kdtree);
	// Set the intensity gradients to use.
	rift.setInputGradient(gradients);
	// Radius, to get all neighbors within.
	rift.setRadiusSearch(0.02);
	// Set the number of bins to use in the distance dimension.
	rift.setNrDistanceBins(4);
	// Set the number of bins to use in the gradient orientation dimension.
	rift.setNrGradientBins(8);
	// Note: you must change the output histogram size to reflect the previous values.

	rift.compute(*descriptors);

	return 0;
}


NARF

The Normal Aligned Radial Feature is the only descriptor here that does not take a point cloud as input. Instead, it works with range images. A range image is a common RGB image in which the distance to the point that corresponds to a certain pixel is encoded as a color value in the visible light spectrum: the points that are closer to the camera would be violet, while the points near the maximum sensor range would be red.

NARF also requires us to find suitable keypoints to compute the descriptor for. NARF keypoints are located near an object's corners, and this also requires to find the borders (transitions from foreground to background), which are trivial to find with a range image. Because of this lengthy pipeline, I will describe the whole process in different sections.

Obtaining a range image

Because we always work with point clouds, I will now explain how you can convert one into a range image, in order to use it for the NARF descriptor. PCL provides a couple of handy classes to perform the conversion, given that you fill the camera data correctly.

A range image can be created in two ways. First, we can use spherical projection, which would give us an image similar to the ones produced by a LIDAR sensor. Second, we can use planar projection, which is better suitable for camera-like sensors as the Kinect or the Xtion, and will not have the characteristic distortion of the first one.

Spherical projection

The following code will take a point cloud and create a range image from it, using spherical projection: 

#include <pcl/io/pcd_io.h>
#include <pcl/range_image/range_image.h>
#include <pcl/visualization/range_image_visualizer.h>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// Parameters needed by the range image object:

	// Angular resolution is the angular distance between pixels.
	// Kinect: 57° horizontal FOV, 43° vertical FOV, 640x480 (chosen here).
	// Xtion: 58° horizontal FOV, 45° vertical FOV, 640x480.
	float angularResolutionX = (float)(57.0f / 640.0f * (M_PI / 180.0f));
	float angularResolutionY = (float)(43.0f / 480.0f * (M_PI / 180.0f));
	// Maximum horizontal and vertical angles. For example, for a full panoramic scan,
	// the first would be 360º. Choosing values that adjust to the real sensor will
	// decrease the time it takes, but don't worry. If the values are bigger than
	// the real ones, the image will be automatically cropped to discard empty zones.
	float maxAngleX = (float)(60.0f * (M_PI / 180.0f));
	float maxAngleY = (float)(50.0f * (M_PI / 180.0f));
	// Sensor pose. Thankfully, the cloud includes the data.
	Eigen::Affine3f sensorPose = Eigen::Affine3f(Eigen::Translation3f(cloud->sensor_origin_[0],
	                                                                  cloud->sensor_origin_[1],
	                                                                  cloud->sensor_origin_[2])) *
	                                                                  Eigen::Affine3f(cloud->sensor_orientation_);
	// Noise level. If greater than 0, values of neighboring points will be averaged.
	// This would set the search radius (i.e., 0.03 == 3cm).
	float noiseLevel = 0.0f;
	// Minimum range. If set, any point closer to the sensor than this will be ignored.
	float minimumRange = 0.0f;
	// Border size. If greater than 0, a border of "unobserved" points will be left
	// in the image when it is cropped.
	int borderSize = 1;

	// Range image object.
	pcl::RangeImage rangeImage;
	rangeImage.createFromPointCloud(*cloud, angularResolutionX, angularResolutionY,
	                                maxAngleX, maxAngleY, sensorPose, pcl::RangeImage::CAMERA_FRAME,
	                                noiseLevel, minimumRange, borderSize);

	// Visualize the image.
	pcl::visualization::RangeImageVisualizer viewer("Range image");
	viewer.showRangeImage(rangeImage);
	while (!viewer.wasStopped())
	{
		viewer.spinOnce();
		// Sleep 100ms to go easy on the CPU.
		pcl_sleep(0.1);
	}
}

Here you can see an example of the output range image:

Range image of a point cloud, using spherical projection.


Planar projection

As mentioned, planar projection will give better results with clouds taken from depth camera: 

#include <pcl/io/pcd_io.h>
#include <pcl/range_image/range_image_planar.h>
#include <pcl/visualization/range_image_visualizer.h>

int
main(int argc, char** argv)
{
	// Object for storing the point cloud.
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile<pcl::PointXYZ>(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// Parameters needed by the planar range image object:

	// Image size. Both Kinect and Xtion work at 640x480.
	int imageSizeX = 640;
	int imageSizeY = 480;
	// Center of projection. here, we choose the middle of the image.
	float centerX = 640.0f / 2.0f;
	float centerY = 480.0f / 2.0f;
	// Focal length. The value seen here has been taken from the original depth images.
	// It is safe to use the same value vertically and horizontally.
	float focalLengthX = 525.0f, focalLengthY = focalLengthX;
	// Sensor pose. Thankfully, the cloud includes the data.
	Eigen::Affine3f sensorPose = Eigen::Affine3f(Eigen::Translation3f(cloud->sensor_origin_[0],
	                                                                  cloud->sensor_origin_[1],
	                                                                  cloud->sensor_origin_[2])) *
	                                                                  Eigen::Affine3f(cloud->sensor_orientation_);
	// Noise level. If greater than 0, values of neighboring points will be averaged.
	// This would set the search radius (i.e., 0.03 == 3cm).
	float noiseLevel = 0.0f;
	// Minimum range. If set, any point closer to the sensor than this will be ignored.
	float minimumRange = 0.0f;

	// Planar range image object.
	pcl::RangeImagePlanar rangeImagePlanar;
	rangeImagePlanar.createFromPointCloudWithFixedSize(*cloud, imageSizeX, imageSizeY,
	                                                   centerX, centerY, focalLengthX, focalLengthX,
	                                                   sensorPose, pcl::RangeImage::CAMERA_FRAME,
	                                                   noiseLevel, minimumRange);

	// Visualize the image.
	pcl::visualization::RangeImageVisualizer viewer("Planar range image");
	viewer.showRangeImage(rangeImagePlanar);
	while (!viewer.wasStopped())
	{
		viewer.spinOnce();
		// Sleep 100ms to go easy on the CPU.
		pcl_sleep(0.1);
	}
}
Range image of a point cloud, using planar projection.


If you prefer to do the conversion in real time while you inspect the cloud, PCL ships with an example that fetches an "openni_wrapper::DepthImage" from an OpenNI device and creates the range image from it. You can adapt the code of the example example from tutorial 1 to save it to disk with the function pcl::io::saveRangeImagePlanarFilePNG().


Go to root: PhD-3D-Object-Tracking

Links to articles:

PCL/OpenNI tutorial 0: The very basics

PCL/OpenNI tutorial 1: Installing and testing

PCL/OpenNI tutorial 2: Cloud processing (basic)

PCL/OpenNI tutorial 3: Cloud processing (advanced)

PCL/OpenNI tutorial 4: 3D object recognition (descriptors)

PCL/OpenNI troubleshooting

Retrieved from "https://robotica.unileon.es/index.php?title=PCL/OpenNI_tutorial_4:_3D_object_recognition_(descriptors)&oldid=3408"